抽象曲面的坚韧探险家

Maryam Mirzakhani不朽的工作建立了拓扑，几何和动力系统深深的联系

当她还是一个8岁的小女孩时，Maryam Mirzakhani（玛丽亚姆·米尔札哈尼）就时常想象做为一个了不起的女孩的传奇故事。每天晚上睡觉前，她的女主人公会成为市长，周游世界或履行其他一些伟大的使命。

时至今日，Mirzakhani--这名37岁的斯坦福大学数学教授--仍然在她心里撰写着复杂的故事。伟大的志向并没有改变，但现在的主人公是双曲曲面，模空间和动力系统。她说，在某种程度上，做数学研究感觉就像写一本小说。“有许多不同的人物，你试着去更好地了解他们，”她说 “但随着事情的发展，当你回头看每一个人物时，却与你的第一印象完全不同。”

虽然故事线往往需要数年才能展开，但无论心中的人物去哪里，这位伊朗数学家都时刻追随。虽然身材娇小，但是不屈不挠，Mirzakhani在数学家中有着用顽强的毅力去解决自己领域最困难问题的美誉。Mirzakhani的博士导师哈佛大学Curtis McMullen（柯蒂斯·麦克马伦）说：“当涉及到数学，她有一种初生牛犊不怕虎的雄心。”

Mirzakhani声音低沉而稳重，有一双灰蓝色的眼睛，充满了坚定不移的自信。她性情平静，很谦虚。当被问及如何描述她对一个特殊的研究问题的贡献时，她笑了笑，犹豫了一下，最后说：“说实话，我不认为我做出了一个非常重大的贡献。”当一封周二到的电子邮件说她将获得被广泛认为是数学中最高荣誉的-菲尔兹奖时（2014年8月13日在韩国首尔国际数学家大会颁发）--她还以为发送该邮件的帐户遭到了黑客的攻击。

其他数学家却总是喜形于色地描述Mirzakhani的工作。她的博士论文 – 数双曲曲面上圈的个数--“煞是壮观”他的合作者芝加哥大学数学教授Alex Eskin（亚历克斯·埃斯金）说“那是一种你马上可以写进教科书的数学。”

芝加哥大学的数学家Benson Farb说，Mirzakhani一个非常新的贡献是她和Eskin在与台球桌有关的抽象曲面的动力系统上进行的不朽的合作，一个在Mirzakhani的竞争激烈的领域等候了十年的定理。

德黑兰

还是一个成长在德黑兰的孩子时，Mirzakhani并没有打算成为一名数学家。她的主要目标只是读每一本她能找到的书。她还观看了著名的女性如居里夫人和海伦·凯勒的电视传记，后来又阅读了描写梵高生活的小说《渴望生活Lust for Life》。这些故事给了她一个未成型的梦想：也许成为一名作家就是在做生命中一些伟大的事。

Mirzakhani读完小学时正逢伊朗和伊拉克战争就要结束，此时对于有积极性的学生机会是开放的。她通过分班测试进入了由伊朗全国特殊人才发展组织管理的德黑兰Farzanegan女子中学。 “我想我是幸运的一代，”她说。“在我十几岁的时候，时局变得更加稳定。”

刚到新学校的第一个星期里，她就遇到了一生的挚友Roya Beheshti（罗亚·贝赫什提）, 其人现在也是华盛顿大学圣路易斯分校一名数学教授。 做为孩子，她俩探索着学校附近拥挤商业街的书店，逛起来的确很累，于是她们随机选择书籍购买。“现在，这听起来很奇怪，”Mirzakhani说。“但书真的很便宜，所以我们只管买。”

让她气馁的是，那年Mirzakhani在数学课表现很差。她的数学老师不认为她特别有才华，这打击了她的信心。在那个年代，“其他人怎么看你非常的重要，”Mirzakhani说。“我失去了对数学的兴趣。”

一年后，Mirzakhani遇到了一个非常鼓舞人心的老师，而且，她的表现也变得非常的出色。Beheshti说：“从第二年开始，她成了一个明星。”

Mirzakhani进了Farzanegan女子高中。在那里，她和Beheshti得到了当年的全国计算机编程比赛选拔试题，这些试题用来确定那些高中学生将参加国际信息学奥林匹克竞赛。 Mirzakhani和Beheshti想了这些问题好几天，并设法解决了六个中的三个。尽管竞赛中的学生必须在三个小时内完成比赛，Mirzakhani也很高兴能够解决其中的任何问题。

Mirzakhani和Beheshti希望发现她们在类似的比赛的能力，她们一起去见了学校的校长，要求她安排和男子高中一样的奥数课程。“学校的校长性格非常坚韧”Mirzakhani回忆道“如果我们真的想要，她就会设法办到。”事实上，伊朗的国际数学奥林匹克队从来没有派出过一个女孩，Mirzakhani说：“她的心态是非常积极和乐观的--那就是‘你可以做到这一点，即使你是第一个’。”Mirzakhani说“我认为这种信念很大的影响了我的生活。”

1994年，当Mirzakhani 17岁时，她和Beheshti进入了伊朗数学奥林匹克竞赛国家队。Mirzakhani在国际数学奥林匹克竞赛中的得分让她赢得了一枚金牌。次年，她又参加了，并且取得了一个满分金牌。 在竞赛的激励下，Mirzakhani深深地爱上了数学，她说：“为了发现数学的美，你必须花一些精力和努力。”

即使在今天，法国巴黎狄德罗 - 巴黎七大的Anton Zorich（安东·卓里奇）说，“Mirzakhani 给我的印象上是一个对发生在她身边的一切数学都感到绝对兴奋那个17岁的女孩。”

哈佛

奥数金牌并不总是意味着数学研究上的成功，1998年菲尔兹奖得主McMullen观察道“在这些竞赛中，人们精心打造了一个有巧妙的解的问题，但在研究中，也许问题根本没有解。”不像许多的奥林匹克高分选手，他说，Mirzakhani“能够形成她自己的视野。”

1999年， 在德黑兰的谢里夫大学完成数学本科学位之后，Mirzakhai去哈佛大学读研，在那里她开始参加McMullen的讨论班。起初，她不明白很多他说的东西， 但仍然被双曲几何之美迷住了。她开始去McMullen的办公室，问他一些尖刻的问题，用波斯语涂鸦着笔记。

“她有着一种大胆的想象力，”McMullen回忆说，“她会在她的脑海里构思一个必定可行的虚构的画面，然后来到我的办公室，并描述它。最后，她就转过来对我说，'是吗？“我总是很受宠若惊因为她以为我会知道。”

Mirzakhani迷上了双曲曲面 – 一种具有两个或更多个孔的甜甜圈，其具有非标准的几何形状，大致说来，曲面上每个点都是马鞍形的。双曲甜甜圈不能在普通的空间构造; 它们在一个抽象的意义存在，其距离和角度由一组特定的方程计算。在这类方程决定的曲面上，一个虚构的动物生活经历的每个点都是鞍点。

事实证明，每个多孔甜甜圈可以以无限多的方式赋予一个双曲结构---粗的甜甜圈，细的甜甜圈，或两者的任意组合。在这种双曲曲面被发现一个半世纪以来，它们已经成为几何中的一些中心对象，并联系到很多数学和物理学的分支。

但是，当Mirzakhani开始读研时，一些关于这些曲面上最简单的问题都没有答案。人们关心直线，或双曲曲面上的“测地线”。即使是一个曲面也可以有一个“直”线段的概念：它只是两点之间的最短路径。在双曲曲面上，有些测地线是无限长的，就像在平面上的直线，而其它的闭合起来成了一个圈，像地球上的经线和赤道。

当测地线的长度增长时，给定长度的双曲曲面的闭测地线的数量呈指数级增长。大多数这些测地线在它们光滑封闭前和自己相交很多次，但其中一小部分，称为“简单”测地线，永远不和自己相交。Farb说，简单的测地线是“是解锁整个曲面结构和几何形状的关键”。

然而，数学家不知道双曲曲面上究竟有多少给定长度的简单的闭测地线。在闭测地线中，简单的闭测地线“奇迹发生的时间是沧海一粟，”Farb说。因此，准确地计算它们是非常困难的：“失之毫厘，谬之千里”他说。

在她2004年完成的博士论文中，Mirzakhani回答了这个问题，得到了随长度L变大时，长为L的简单的测地线数量增长的公式。沿着这条路，她建立了与其他两个主流研究问题的联系，并解决了它们。一个是有关所谓的“模空间”--一给定曲面上所有可能的双曲结构--的体积公式。另一个是一个旧猜想令人惊讶的新证明，此猜想是关于与弦论有关的模空间的某些拓扑量，是由新泽西州普林斯顿高等研究院的物理学家Edward Witten（爱德华·威腾）提出的。Witten猜想是如此的困难，以至于第一个证明它的数学家–靠近巴黎的法国高等科学研究所的Maxim Kontsevich（马克西姆·孔采维奇） – 部分由于这个工作被授予1998年的菲尔茨奖。

Farb说，“解决所有这些问题是一个大事，将它们联系起来也是一个大事。”Mirzakhani都做了。

Mirzakhani论文最终成为发表在数学的三个顶级期刊的三篇论文：Annals of Mathematics, Inventiones Mathematicae 和 Journal of the American Mathematical Society。大多数数学家永远不会做出这样好的东西，Farb说-“而她在她的博士论文中就做到了。”

“宏伟的作品”

Mirzakhani喜欢形容自己做研究非常慢。不像有些解决问题迅速的数学家，她被那些她可以思考多年的深层次的问题所吸引。她说“几个月或几年后，你会看到一个问题非常不同的方面”。有些问题，她一直思考了十年以上。 她说“我仍然无从下手”。

Mirzakhani的节奏不会被那些迅速解决问题的数学家打乱。 “我不容易失望，”她说。 “在某种意义上，我非常有信心。”

她缓慢而沉着的方式也体现在她生活的其它方面。有一天，当她是一名哈佛研究生时，她未来的丈夫Vondrak（冯德拉克），当时也是麻省理工学院的研究生，就体会到 Mirzakhani的这一点，他们相约去跑步 “她非常娇小，我的体型很好，所以我想我会做的很好，起初，我领着她”，现在是一名圣何塞加利福尼亚州IBM Almaden研究中心理论计算机科学家的Vondrak回忆说“但她从来没有减慢速度。半小时后，我跑不动了，但她仍然以同样的速度运行。“

当她思考数学时，Mirzakhani不断涂鸦，画曲面和其它与她研究相关的图像。Vondrak说，“她在地上铺上一些巨大的纸片，花几个小时一遍又一遍地画一些对我来说同样的画面，”他补充说，她的家庭办公室随意散布着论文和书籍。他说“我不知道她怎么可以像这样工作，但最后总能解决问题”。他推测，也许这是因为“她正在研究的问题是如此抽象和复杂，她无法提供一步步的逻辑的链条，而必须做出很大的跳跃。”

涂鸦可以帮助她集中注意力，Mirzakhani说。人们在思考一个困难的数学题时“你不想写下所有细节，”她说。 “但是，在画的过程中可以帮助你以某种方式理解它们。”Mirzakhani说，她3岁的女儿，Anahita（安娜希塔），常常感叹：“哦，妈妈再画！”当她看到数学家涂鸦时 “也许她认为我是一个画家，”Mirzakhani说。

Mirzakhani的研究涉及到数学的许多领域，包括微分几何，复分析和动力系统。 “我喜欢穿越人们设置在不同领域之间假想的边界- 这将令人耳目一新，”她说。在她的研究领域，“有很多工具，但是你不知道哪一个会起作用，”她说。 “我乐于尝试去建立它们之间联系。”

McMullen说，有时Mirzakhani建立的联系是相当令人兴奋的。以2006年为例，她通过用类似于一个撞击滑动型地震的机制，攻克了双曲曲面的几何形状变形时，将会发生什么的问题。 在Mirzakhani的工作之前，“这个问题完全不可触及，”麦克马伦说。但只用了一行的证明，他说，“她建造这个完全不清楚的理论和另一个完全清楚的理论之间的桥梁。”

2006年，Mirzakhani开始了她与Eskin富有成效的合作，他也认为她是他最喜欢的合作者之一。 “她很乐观，很有感染力”他说。 “当你和她在一起工作时，你会感到你更有可能去解决那些起初看来毫无希望的问题。”

在几次合作后，Mirzakhani和Eskin决定解决他们领域中一个最大的公开问题。它关注一个台球在任何多边形形状的台球桌上运动的行为，只要求这种多边形的角的角度是有理数。台球提供了一些最简单的动力系统的例子 - 即按照给定的规则随时间演化的系统 - 但是已经证明台球的行为出乎意料的复杂。

“有理多边形球台的研究开始于一个世纪以前，当时一些物理学家围坐在一起说，'哦，让我们来看看一个台球如何在一个三角形球台上运动” 斯坦福大学博士后研究员Alex Wright（亚历克斯·怀特）说。 “本来他们认为他们会在一周内完成，但100多年后，我们仍在考虑这个问题。”

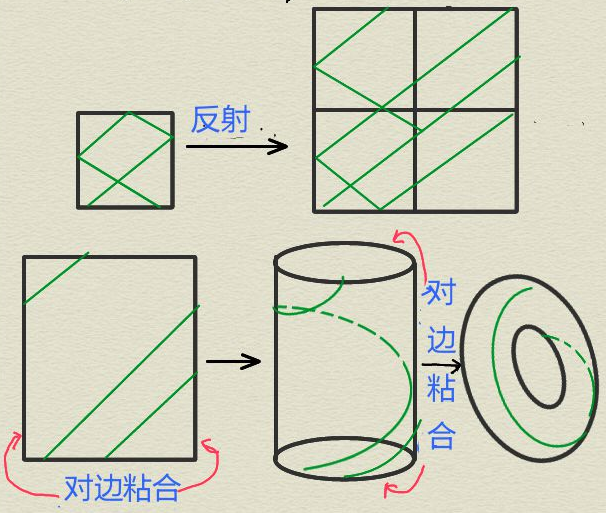
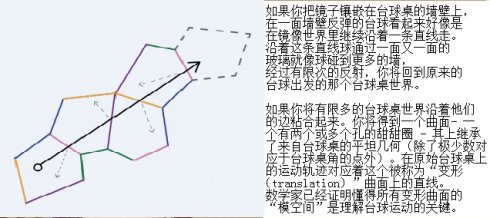
为了研究台球的长期运动轨迹，一个有用的方法是想象沿运动轨迹方向慢慢地压扁台球桌，以至在给定时间内，我们可以看到更多的台球运动轨迹。原始的台球桌变成了一系列新的台球桌，这个变换也可以想象成在数学家所说的模空间上航行，这个模空间是由给定边的数目的所有可能的台球桌组成的。通过将每个台球桌变成一个被称为“变形（translation）曲面”的抽象曲面，数学家可以通过了解所有变形曲面组成的模空间来分析台球的运动。研究人员已经证明通过了解压扁台球桌运动在模空间形成的“轨道”（译者注：Teichmüller测地流）有助于回答许多有关原始台球桌的问题。

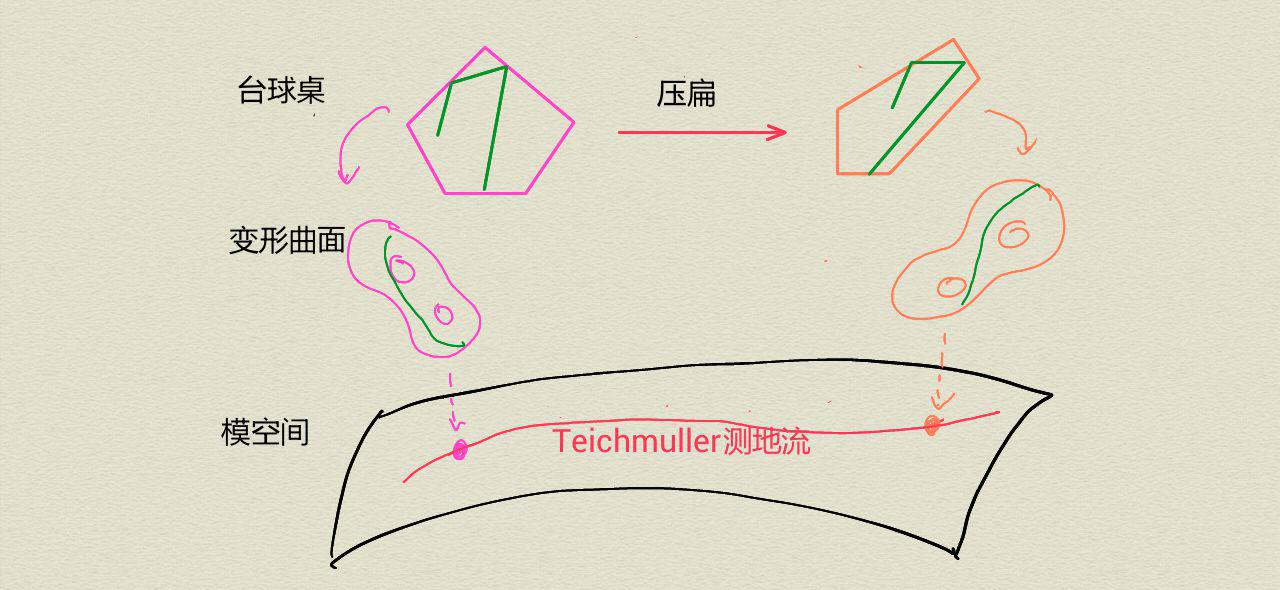
表面上来看，这个轨道可能是一个非常复杂的对象 -例如一个分形。但是2003年，麦克马伦证明当变形曲面是一个双孔（“亏格二”）甜甜圈时情形并不复杂：每个轨道填满整个空间或者该空间的一些被称为子流形的简单的子集。

McMullen的结果被人们誉为一个巨大的进步。他回忆说，然而在他的论文发表之前，那时还是一名研究生Mirzakhani来到他的办公室，问：“为什么你只做双孔甜甜圈？”

“她就是这样一个人，”他说。 “一旦看到了什么暗示，她就想了解的更清楚。” 

经过多年的努力，在2012年和2013年，Mirzakhani和Eskin，部分工作是与美国德克萨斯大学奥斯汀分校的Amir Mohammadi（穆罕默德·阿米尔）的合作，将McMullen的结果成功地推广到所有表面有两个以上孔的甜甜圈。Zorich补充说，他们的分析是“宏伟的作品”，其影响远远超出了台球。模空间“在过去30年来已经被深入地研究，”他说，“但是关于它的几何我们所知甚少。”

Mirzakhani和Eskin的作品是“一个新时代的开始，”Wright说，他花了几个月时间去研究他们的172页的论文说。“就像我们试着去砍伐一片红木林，以前只有一把斧头用，但现在他们已经发明了一种链锯，”。他们的工作已经得到了应用 - 例如，了解复杂的镜像房中保安员的视线问题。

在Mirzakhani和Eskin的文章中，“在每一层难度和思想之下躺着隐藏的更深的另一个，” Wright在一封电子邮件中写道。 “当我到达中心的时候，我惊讶于他们所建立的机制。”

是Mirzakhani的乐观和坚韧使得这一切顺利进行，Eskin说，“有时候有挫折，但她从不惊慌失措，”。

即使Mirzakhani自己也很惊讶，现在回想起来，他们还是坚持了下来了 “如果我们知道事情会这么复杂，我想我们会放弃，”她说。然后，她停顿了一下。 “我不知道;其实，我真的不知道，“她说。 “我不轻易放弃。”

下一章

Mirzakhani是78年来首位获得菲尔茨奖的女性。在数学中性别比例失衡是长期和普遍的，而菲尔兹奖，尤其是不适合许多女性数学家的职业生涯。它被限制在授予年龄小于40岁的数学家，而正是这段时间里，许多妇女不得不远离她们的职业去养育子女。

虽然如此，Mirzakhani相信未来会有更多的女性获得菲尔兹奖。她说“真的有很多伟大的女数学家做伟大的事情”。

她虽然感到非常荣幸被授予菲尔茨奖，但并不打算成为女性在数学中的公众形象。她儿时的梦想已经被这喜出望外的奖项所实现，她说，但今天，她更渴望将注意力从这些成就转移，以至于可以专注于研究工作。

Mirzakhani已经有了一个宏伟计划，将写就她数学故事的下一个篇章。她已经开始与Wright合作，尝试建立起变形曲面轨道可以填补的各种几何集合的完整列表。Zorich写道，这样的分类对于理解台球和变形曲面将是一个“魔杖”。

这是个不小的任务，但Mirzakhani多年来已经习惯了从大处着眼。 “虽然有点棘手，但你必须忽略低悬的果实，”她说。 “我不确信这是做事情的最好办法，事实上 - 你在自己前进的道路上折磨着自己”，但她喜欢，她说。 “生活本来就不容易。”

译者补充：

今年另一菲尔兹奖获得者Artur Avila的部分获奖工作也与台球的动力系统有关。后两幅图由译者提供。

本文译者：

于飞，ylzzcom永利总站线路检测教师，在Teichmüller测地流领域工作的两位华人之一（另一位是波士顿学院的陈大卫）。

在此领域的成果包括首先引入代数几何的稳定性，完全证明Kontsevich（菲尔兹奖）-Zorich一个十多年的猜想，以及提出一个比较代数几何稳定性和动力系统稳定性的新猜想。

译自Simons基金会

http://www.simonsfoundation.org/quanta/20140812-a-tenacious-explorer-of-abstract-surfaces/